


| Title: | Location | K-4 | 5-8 | 9-12 | Description | Discipline |
| Shepard's Tones | SoundGarden | Why do these tones always go up in pitch? |
This illusion was invented by Roger Shepard, a psychologist, in 1964. He used a computer to create a series of tones, or a scale, that seems to rise forever.
TIP: although you can use the speakers on your multimedia computer, a Make sure the volume isn't too loud!
![]()
BarberShop Pole – Image Courtesy VR-Mall
Can you perceive the point where these tones jump down and repeat the cycle?
Hands-On! Activity
Make Your Own Barbershop Pole
The Shepard's Tone illusion does in sound what the old-fashioned barbershop pole does visually, e.g. seemingly rise forever. This activity uses a graph of the of the Shepard's Tones' frequencies to create the same effect as the barbershop pole. The graph is called a spectrogram. It shows the Shepard Tone's frequencies changing through time. Can you see where they drop down and start to rise again in a cycle?
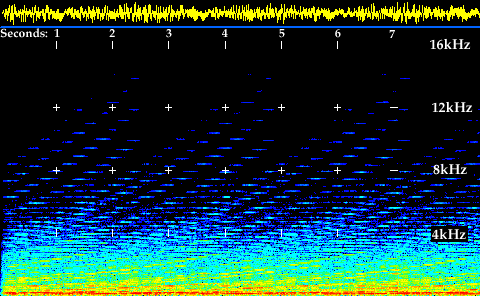
Spectrogram of the Eight Shepard's Tones
Materials needed:
- a pair of scissors
- clear tape
- a pen or magic marker
- pencil with eraser
- sewing needle
- 12" any color thread
- a print-out of the spectrogram on this page.
To Do:
- Print out this page, if possible use the print preview function to select the page that contains just the spectrogram, so you don't waste paper.
- Cut out the top 1.5 inches of the Shepard's Tones spectrogram.
- Tape the bottom edge to the pencil to secure the paper.
- Now wrap the paper around the pencil and tape the top, middle, and bottom.
- Carefully thread the sewing needle so you have 6" of thread
- Carefully insert the sewing needle into the middle of the eraser
- Trace a single line with a pen or magic marker beginning at the bottom. It should go all the way to the top without breaking the line.
- Hold the pencil by the thread and slowly twirl it, observe beginning with the bottom of the pencil. What happens?
What's the point?
The 'Make Your Own Barbershop Pole' activity provides a visual representation of what you hear, the ever-rising sound to the Shepard's tones.
The point here is that your brain uses two main features to perceive the effects of this illusion:
- a sensitivity to changes in rising pitch,
- a sensitivity to volume changes in these pitches.
Each Shepard tone is made of eight different tones, all an octave apart. They cover a frequency range that is similar to that covered by all of the keys on the piano.

As the tones play, they rise in pitch, gradually getting higher until they rise to half of their original frequency. Then they jump back down to their original frequency and repeat the cycle. You'd think that you could perceive where this jump in frequency occurs but that's where the volume changes become a factor.
Each of the eight tones has a unique volume curve, getting gradually louder or softer. The key is that when any tone finishes rising in pitch, its volume matches that of the next tone beneath it. So when the lower tone reaches the end of the cycle, its volume matches that of the higher tone.
Since these changes occur gradually and over a wide spectrum of sound, the result is a seamless transition in the cycle, just like the "barbershop pole" you made from its spectrogram.
Follow this link for more information on how to create your own spectrograms with free software. Use the BACK button on the top left of your browser to return to this page.
Just for Fun!
What do you think would happen if the set of tones had only six of the eight tones playing? Would you be able to hear the volume changes?
 (14") – listen to rising tones.
(14") – listen to rising tones.- What do you think would happen if we speed up the tones? Is it easier or harder to hear the point where the tones jump down and repeat the cycle? Why?
 (26") – listen to rising tones.
(26") – listen to rising tones.- What do you think would happen if the set of tones had only six of the eight tones playing and we speed up them up as well? Is it easier or harder to hear the point where the tones jump down and repeat the cycle? Why?
 (12") – listen to rising tones.
(12") – listen to rising tones.
What can you conclude about the effect of speed and volume changes on these tones?
What other visual illusions are similar to these tones? [ HINT: think M.C. Escher ]
What other experiments might you try?
More Shepard's Tones Examples
TIP: the links on this page take you places on the Internet that don't have navigational buttons back to this page. If you use them, please use the BACK button on the top left of your browser to return to this page and continue.
 More Shepard's Tones #1 – excellent examples of Shepard's Tones from Norma Welch's site.
More Shepard's Tones #1 – excellent examples of Shepard's Tones from Norma Welch's site. More Shepard's Tones #2 – a clever imagemap that lets you play and
hear individual tones within an octave span.
More Shepard's Tones #2 – a clever imagemap that lets you play and
hear individual tones within an octave span. More Shepard Tones #3 – nice charts and sound examples of the tones.
More Shepard Tones #3 – nice charts and sound examples of the tones.
 More Shepard's Tones #4 – also called 'pitch circularity,' from the Acoustical Society's Auditory demonstration CD.
More Shepard's Tones #4 – also called 'pitch circularity,' from the Acoustical Society's Auditory demonstration CD. Risset's Endless Glissando (aka More Shepard's Tones #5) – this resource has quicktime movies and sound examples that show how the various tones get louder and softer, while changing their pitch.
Risset's Endless Glissando (aka More Shepard's Tones #5) – this resource has quicktime movies and sound examples that show how the various tones get louder and softer, while changing their pitch.
"Certainty generally is illusion,
and repose is not the destiny of man."
– Oliver Wendell Holmes, Jr.
Send your comments to: webteam@cafemuse.com
© 1996 – 2013 NewWorldView, All Rights Reserved.